ALQORITHM
created by George Holm, Pranet Sharma, Brennan Lagasse, Diya Naik, Frank Wong
What is QSP?
Quantum Signal Processing is a type of quantum algorithm that can construct estimations of polynomial functions as a function of e. Quantum signal processing is ideal for NISQ era superconducting hardware since it can be achieved through only single qubit rotations and does not require high error rate two-qubit gates. The phases used to make these graphs, and the outputs themselves have vast applications in quantum algorithms.
How it Works
The most essential components of quantum signal processing involve the signal rotation operator W and the signal processing rotation operator S. The W operator performs an x rotation while S performs z rotations. See Fig. 1, which shows the W and S operators respectively. The signal rotation always rotates through the same angle [theta] while signal processing rotation occurs through a variable angle. These two operators are used as shown in Fig. 1 After we perform this, we can plot the probability of 0s. This can easily be found by measuring the counts of 0s and 1s after all of the RX and RZ gates have been performed. The fraction of 0s can be used to calculate the probability at each point we evaluated the function at. Note that for the following graphs, n corresponds to the 1 plus the degree of the function used to fit the data.

Fig. 1
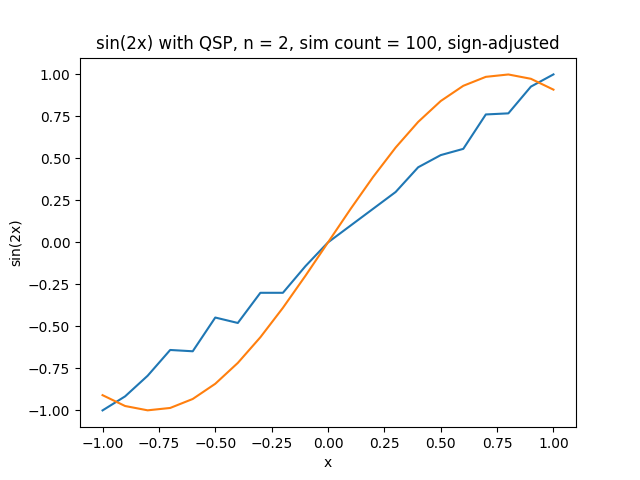
Simulation of what QSP will generate with sin graph on 2 phis
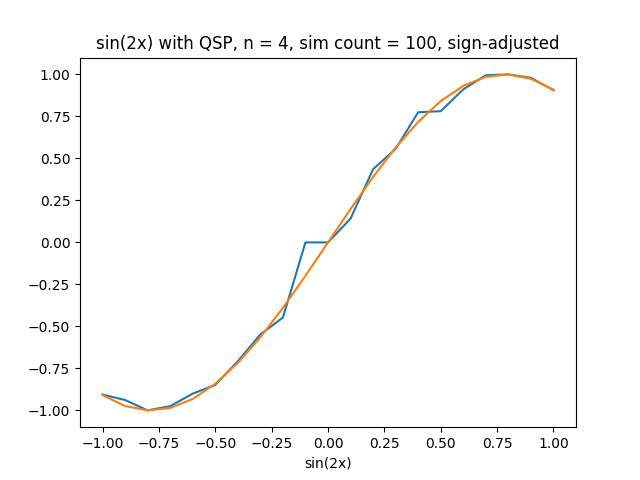
Simulation of what QSP will generate with sin graph on 4 phis
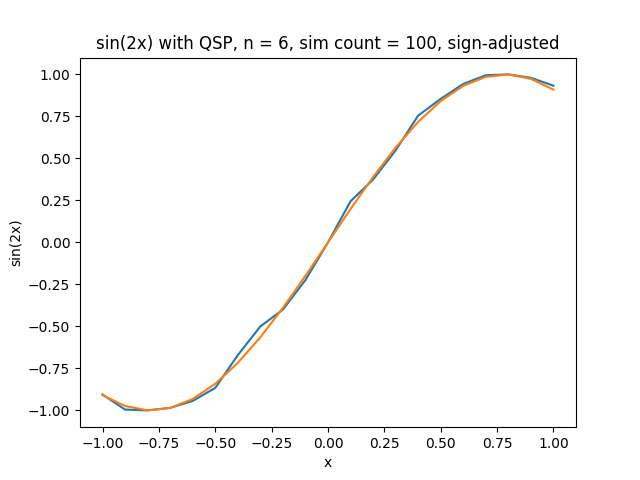
Simulation of what QSP will generate with sin graph on 6 phis
For the simulated graph plotted above from two phis not too great of a fit. This is for a function of degree 1 though, so it makes sense that the QSP doesn’t produce an appropriate graph for the sin function.
For a the simulated graph above now we see a better fit for a function of three degrees. Yet there’s still room for improvement.
Now we get a very good approximation for the sinn function in a simulated quantum computer by just calculating 6 phis, to see how noise will change things on actual quantum hardware we will compare the results below.
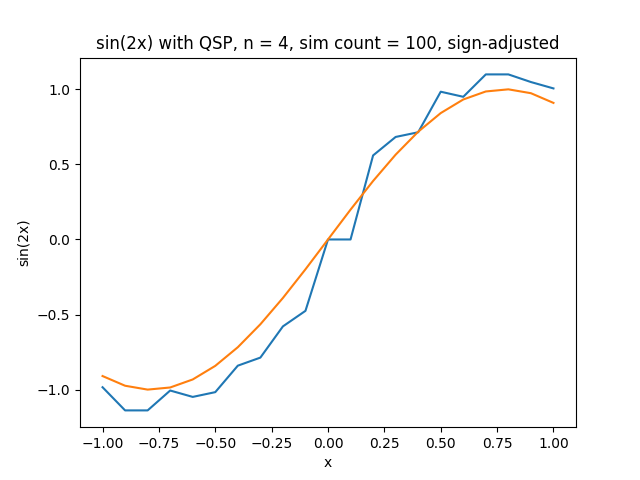
Simulation of what QSP will generate with sin graph on 4 phis
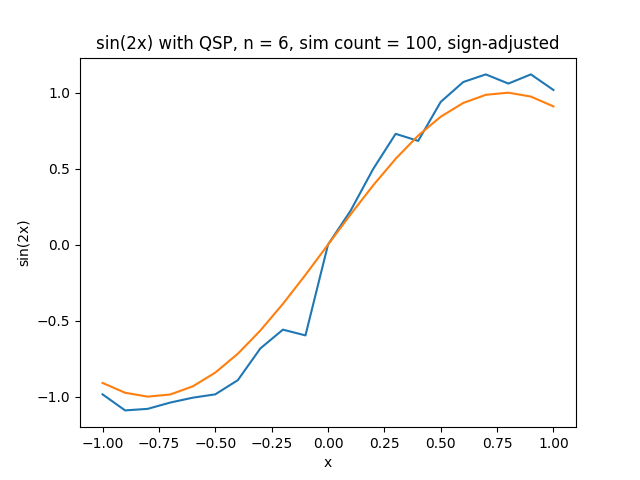
Simulation of what QSP will generate with sin graph on 6 phis
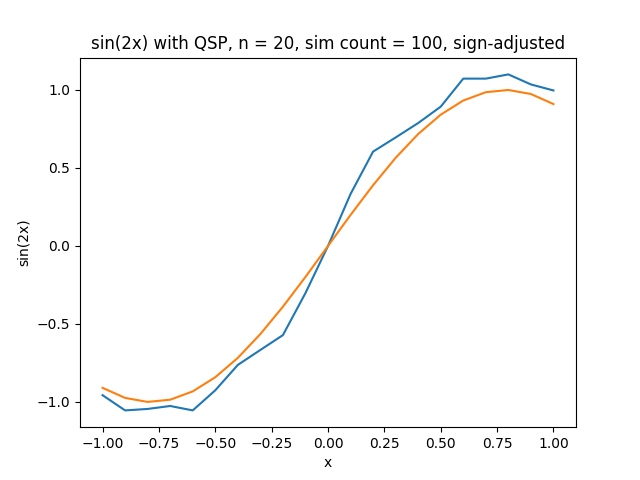
Simulation of what QSP will generate with sin graph on 20 phis
All three graphs above are results from data taken from actual quantum computers at IBM. Note how as more phis are added to the graph, the relative smoothness of our approximation becomes greater. This happens until the noise associated with real qubits messes with the data too much. There is a minimum amount of noise when we compare the function we’re modeling to our actual approximation, which can easily be graphed by plotting the magnitude of difference between the actual and predict values vs. phi.
Learn more from our Jupyter Notebooks here:
- Run your own Jupyter notebook to simulate for your self
- The core of ALQORITHM comes from allowing users to build their own algorithms
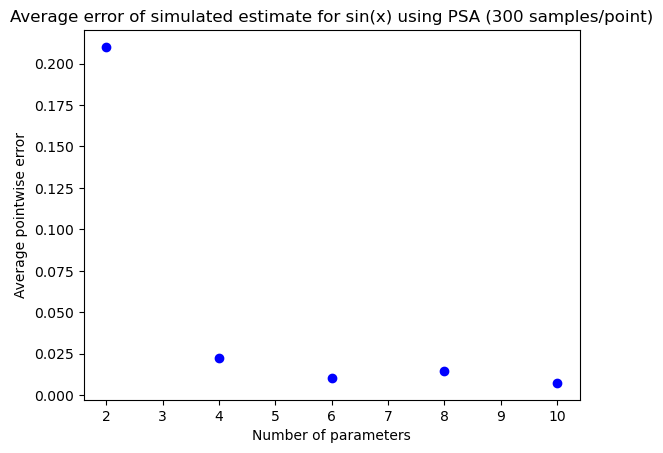
Figure comparing the error of sin function as complexity increases
On the left is a visual that represents the quantum estimations of the sin function error as a function of how many parameters we give the quantum computer. Notice how it seems to trend downwards as we increase complexity, we do not know what the limit of this is, especially in a noisy quantum system.
On the right we have also have a simulation of the function y = 1/x to see what our graphs will look like with other functions, including interesting ones with discontiunity.
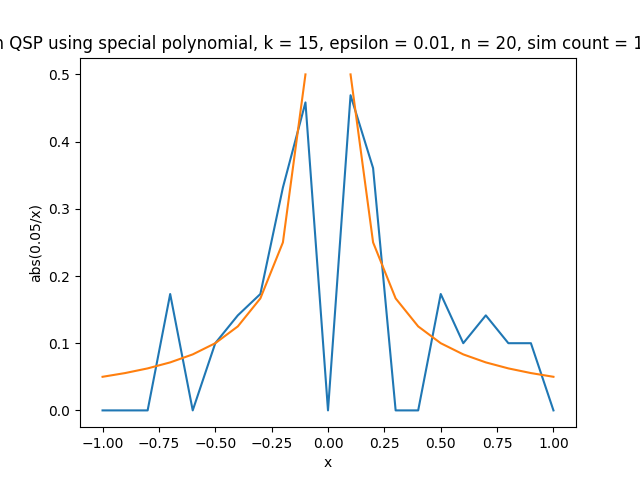
Simulation of function 1/x with 20 points of data
Sources:
[1] A Grand Unification of Quantum Algorithms, John Martyn et. al 2021, (https://arxiv.org/abs/2105.02859) Describes the derivation of QSP and applications, including the amplitude amplification algorithm
[2] (https://github.com/ichuang/pyqsp) Implementation of many of the classical components of the algorithm including optimizing the angles for the algorithm
[3] (https://github.com/alibaba-edu/angle-sequence) Library used in the implementation of pyqsb
[4] Realization of quantum signal processing on a noisy quantum computer (https://arxiv.org/abs/2303.05533) Paper that implements QSP on actual hardware with neutral atoms